数据可视化3N+1冰雹猜想
冰雹猜想是指:一个正整数x,如果是奇数就乘以3再加1,如果是偶数就析出偶数因数2ⁿ,这样经过若干个次数,最终回到1。
无论这个过程中的数值如何庞大,就像瀑布一样迅速坠落。而其他的数字即使不是如此,在经过若干次的变换之后也必然会到纯偶数:4-2-1的循环。据日本和美国的数学家攻关研究,在小于7*10^11的所有的正整数,都符合这个规律。
冰雹猜想来历
1976年的一天,《华盛顿邮报》于头版头条报道了一条数学新闻。文中记叙了这样一个故事:
70年代中期,美国各所名牌大学校园内,人们都像发疯一般,夜以继日,废寝忘食地玩弄一种数学游戏。这个游戏十分简单:任意写出一个正整数N,并且按照以下的规律进行变换:
如果是个奇数,则下一步变成3N+1。
如果是个偶数,则下一步变成N/2。
不单单是学生,甚至连教师、研究员、教授与学究都纷纷加入。
为什么这种游戏的魅力经久不衰?因为人们发现,无论N是怎样一个数字,最终都无法逃脱回到谷底1。准确地说,是无法逃出落入底部的4-2-1循环,永远也逃不出这样的宿命。
这就是著名的“冰雹猜想”。
“4、2、1”黑洞
当你列举出一个数时(0、负数除外的整数),无论它是奇数还是偶数,只要是奇数就将它×3+1,只要是偶数就将它÷2,一直重复循环,最终一定是“4——2——1”结尾。
2022年1月26日,美国世界开放性数学刊物《Advances ln Pure Mathematics》(《纯数学进展》)在2022年第12卷第1期发表了陇西籍硕士、大学教师王茂泽与三位合作者的文章《The Proof of The 3x+1Conjecture》(《3x+1猜想的证明》)。至此, 世界公认的著名数论难题得以破解!
这里我用简单些的方式来说明:
N为正整数。
当N为奇数(单数),N下一步变为3N+1。
当N为偶数(双数),N下一步变为N÷2。
在这样的运算规律下:
当N=1:1,4,2,1,4,2,1...
当N=2:2,1,4,2,1,4,2...
当N=3:3,10,5,16,8,4,2,1...
当N=4:4,2,1,4,2,1,4...
当N=5:5,16,8,4,2,1...
当N=27:27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1...
这里用数据可视化工具来分析“3N+1冰雹”,提供一个新的视角来看待这个问题。
先尝试了利用python的matplotlib模块,方便快速的编程来验证算法。
在直角坐标系,x轴为步数,y轴为运算数值
画出当N=27的“3N+1冰雹”数据图形
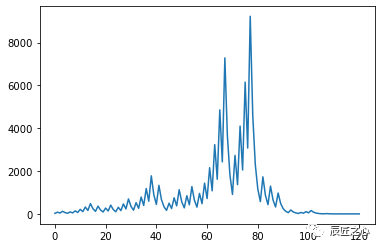
为看数据方便、提升交互性,接下来使用百度的Echarts来编程制作网页html页面。
用直角坐标系,看N=27的“3N+1冰雹”数据图形(点击查看>>>)
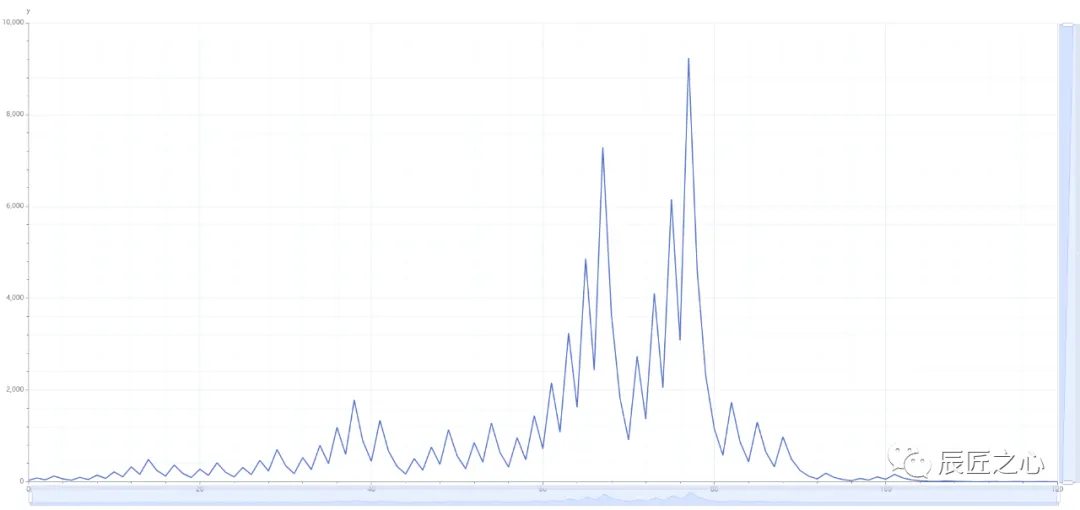
在浏览器里拖动鼠标看数据,发现在当N=27的第111歩时,数据为1,之后继续4-2-1循环。
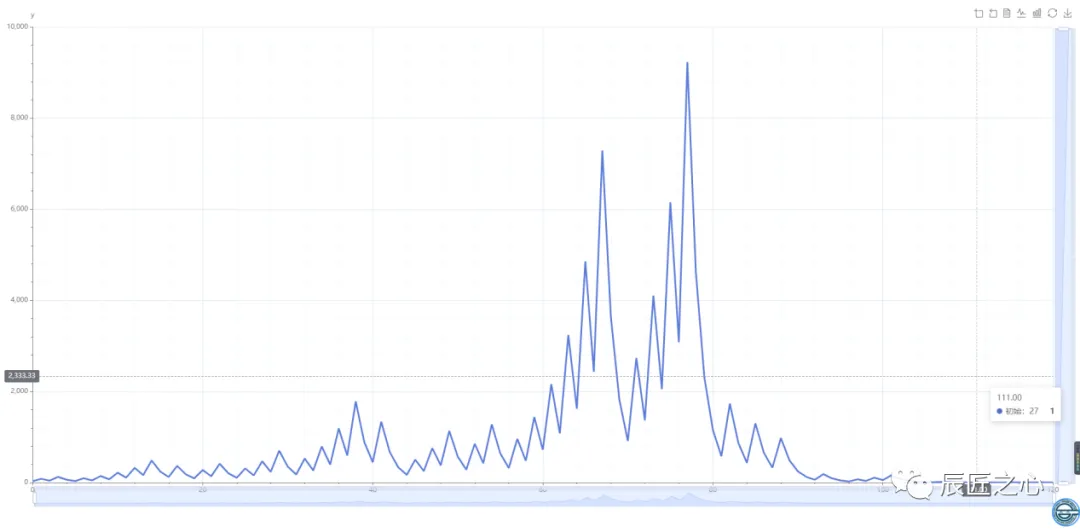
发现在当N=27的第77歩时,数据最大值为9232。
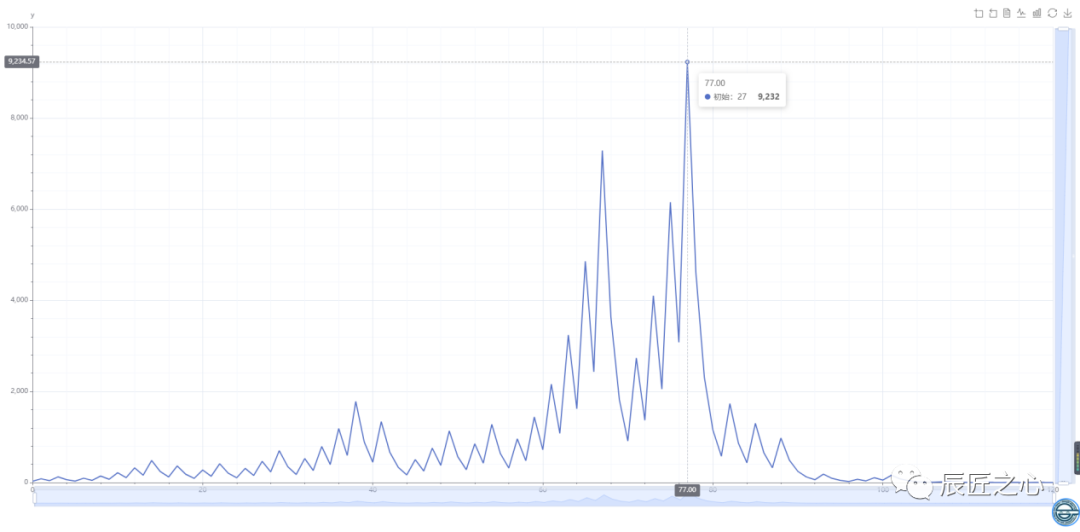
以上是看单个初始值N的“3N+1冰雹”,接下来试试制作多个初始值的图像。
从之前的内容,得知所有“3N+1冰雹”里有4-2-1黑洞,那来画下当N=1,2,4的图像。(点击查看>>>)
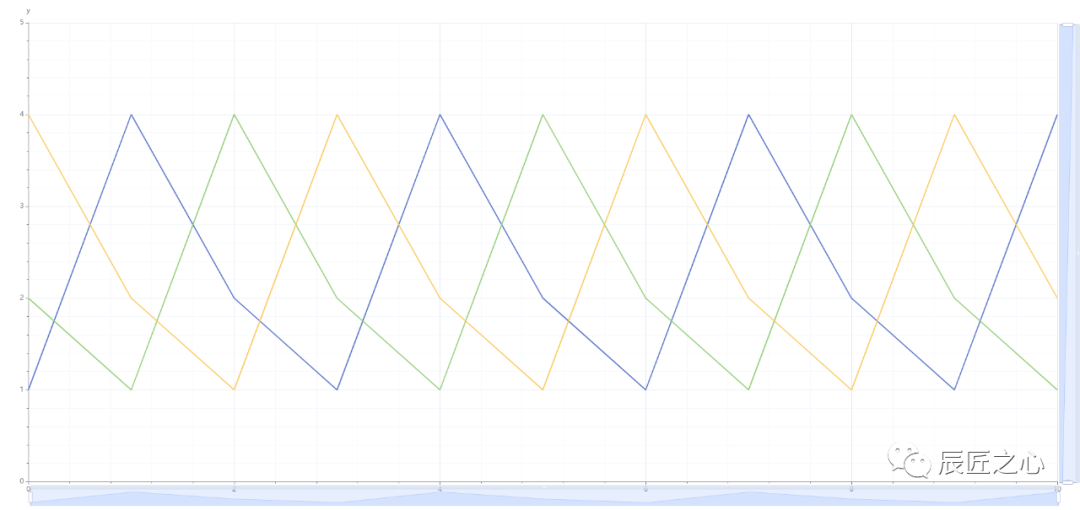
发现这个“黑洞”的形状有点像三相交流电的波形,由3个形状相同、周期为3步但各相差1步的波形组成。还会发现“黑洞”里的各个顶点包涵全部x周也就是全部整数,没有漏洞。
之后再看N=1到10的“3N+1冰雹”图像(点击查看>>>)
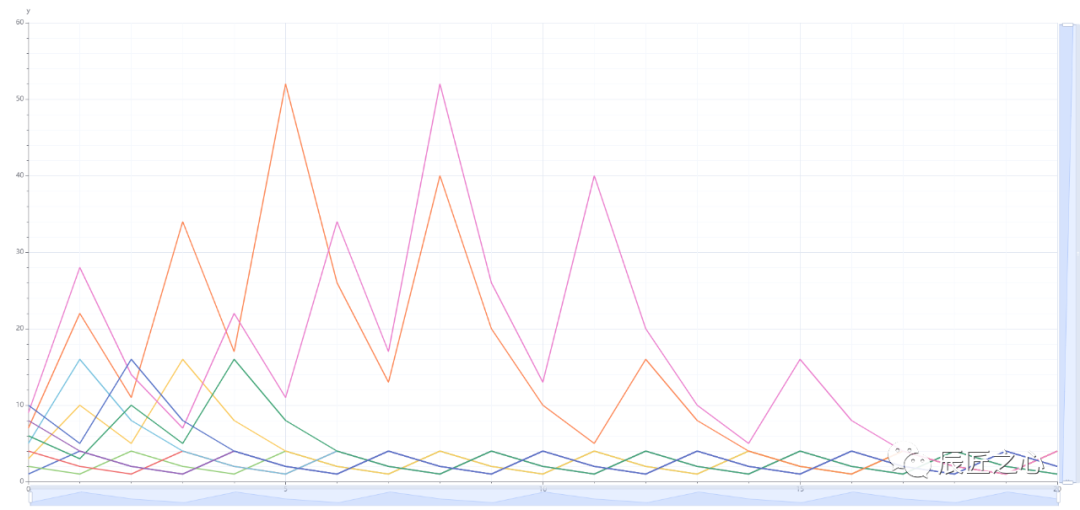
再看N=1到25的“3N+1冰雹”图像(点击查看>>>)
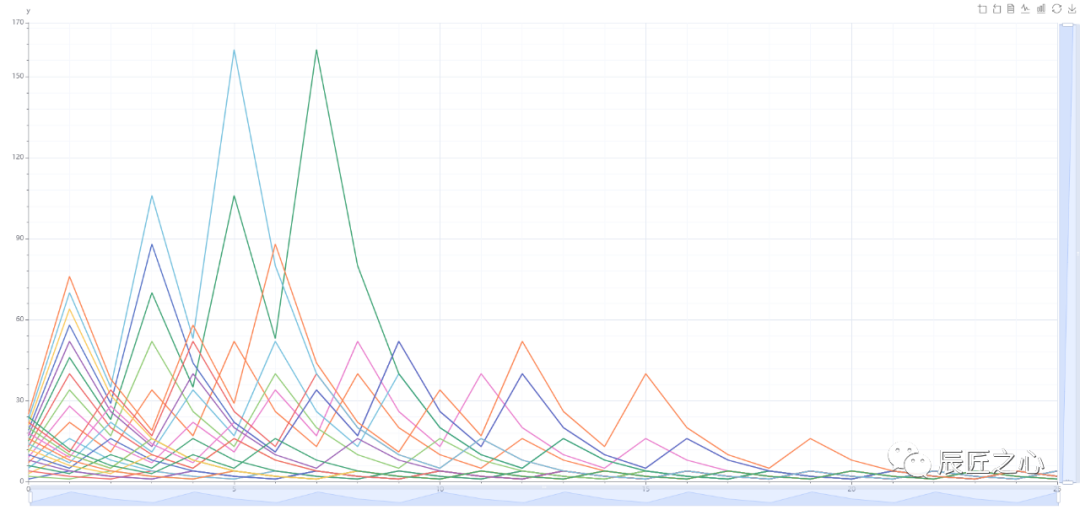
再看N=1到100的“3N+1冰雹”图像(点击查看>>>)
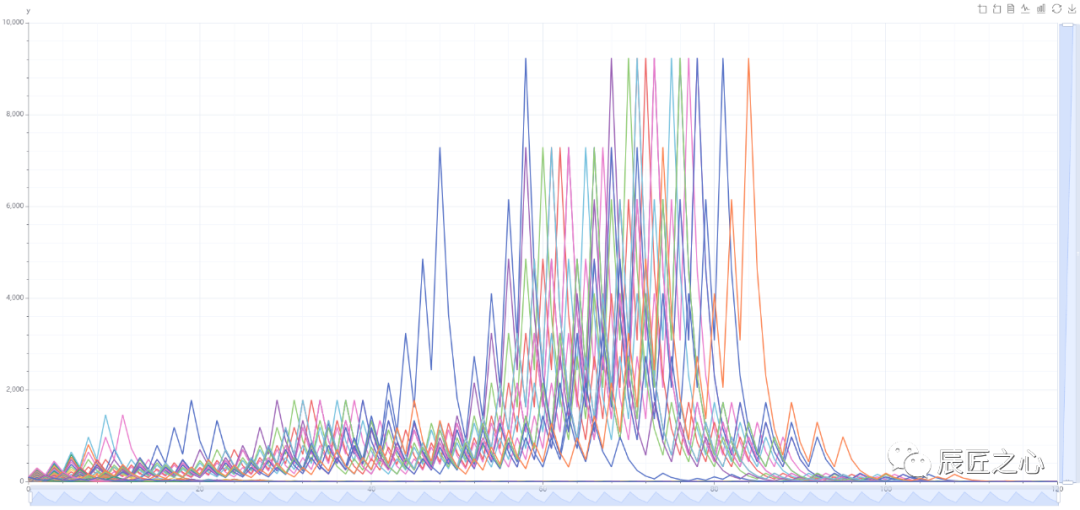
再看N=1到400的“3N+1冰雹”图像(点击查看>>>)
.png)
随着数据越多,页面加载会越来越慢。
会看每个N都会有各不相同的轨迹,最后都会从16-8这个入口坠入4-2-1循环黑洞。
用关系图:
当N=3的图像(点击查看>>>)
.png)
当N=9的图像(点击查看>>>)
.png)
当N=6、9的图像(点击查看>>>)
.png)
通过这样数据可视化这里对“3N+1冰雹”简单归纳:
1、“3N+1冰雹”运行时,在除了4-2-1这三个数的循环黑洞,N是不会遇到与自己相同的数值,这样导致了“3N+1冰雹”不会再有其他数值的循环黑洞。
2、“3N+1冰雹”变化情况:
(1)对于任意N:
每次上升是因为3N+1,上升程度(后值-前值)3N+1-N=2N+1。
每次下降是因为,下降程度(前值-后值)N-N/2=N/2。
(2)考虑2次数据变动:
当N≥3的奇数,经过3N+1上升一次就会变偶数,然后必定 N/2下降一次:
N --> 3N+1-->(3N+1)/2
上升变化程度(后值-前值):(3N+1)/2-N=(N+1)/2
当N变动为4的倍数(偶数)时就会发生2次下降:N --> N/2 --> N/4
下降变化程度(前值-后值):N-N/4=3N/4
比较这上升和下降的系数1/2 < 3/4,会发现总体趋势还是下降。
3、从4-2-1黑洞反向分叉考虑,出口就是16-8。
从16开始会分叉为5(5×3+1=16)和32(32/2=16)
这样就会就某一个歩(x)反推到多个数据(y),某些步数(x)范围也就反推比这个范围更多的数据(y)
4、结尾相似的波形,比如:
当N=3:3,10,5,16,8,4,2,1...
当N=10:10,5,16,8,4,2,1...
当N=5:5,16,8,4,2,1...
会发现:
(1)N=3的波形,包涵N=10、N=5...等的的波形。
(2)N=10的波形比N=3的结尾波形提前1步到4-2-1黑洞,N=5的波形比N=10的结尾波形提前1步到4-2-1黑洞...
(3)N=6和N=9其实是就包涵了N=1到10的波形
.png)
以上就是这里通过pythonh、echarts这样的数据可视化工具,方便地对数据查看,然后再归纳分析,来初步地认识了解“3N+1冰雹”的过程。这里水平有限也就简单说明,欢迎大家交流。
内容分类
联系我们:
公众号:辰匠之心电话:13816242731
QQ:2700181864
Email:contact@v-craftsman.com



